卷积神经网络

申明 ：以下内容总结摘录至B站Up主王木头学科学 的相关视频，本人出于学习目的，学习他的视频内容并选择性的总结和摘录以丰富自己的知识和对卷积神经网络的理解，也就是做笔记

视频链接：理解卷积、卷积操作、再到卷积神经网络，本文章内的其他内容也可以在他的个人主页相关视频中找到

卷积神经网络

什么是卷积？

卷积公式

• 公式如： $$\int_{-\infty}^{+\infty} f(\tau)g(x - \tau) d\tau$$

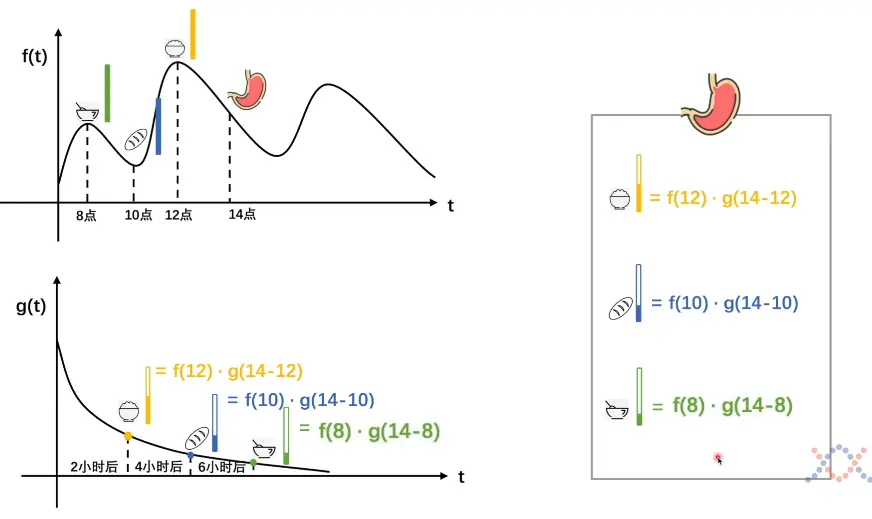
• 结合视频中的例子，有如下解释
  • 函数 $f(\tau)$ 表示一个人的进食情况或者简单的说是在某一时刻（横坐标）人进食的量化即吃了多少东西（纵坐标）
  • $g(x - \tau)$ 则表示这个人的消化情况，反映经过多长时间后某一摄入的食物将消耗至原来的多少（比例)
  • 这两个函数的乘积反映出一个模型：在某一个时刻 $\tau$ 摄入食物，在另一时刻 $x$ 时，该食物在人体内还留存多少，那么求积分则是计算在 $x$ 时刻时，人体内所有食物存量的总和（因为在此之前，可能摄入在不同的时间摄入了不同量的食物，在到达同一时刻它们的剩余量也不尽相同）
  • 积分的上下限是非固定的，需要结合实际问题模型来确定，视频例子则是从0时刻开始到$+\infty $
• 由此我们可以得到卷积公式的物理意义体现在：一个系统具有不稳定的输入 $f$ 以及可以得到稳定的输出 $g$ ，积分求出系统的存量

卷积在计算机的应用

• 对卷积公式应用的拓展延伸，卷积的意义更有深度，体现了在某一个时刻之前周围事物对该事物产生的影响的叠加

卷积神经网络

• 用于图像处理，探究周围像素点对某中心像素点产生的影响（不同像素点的影响贡献度可以不同，并且可以调解）
• 卷积核的不同，对特征提取有不同的效果（卷积核的设置是人为的，赋予了计算机利用神经网络进行学习更强的目的性和主动性）
  • 如下图中两种不同的卷积核能够提取保留出两个不同方向上的图片像素，效果明显；因此卷积核也有过滤器的说法

• 经过卷积核的特征提取/过滤后，将这些保留的特征用于神经网络的输入以进行后续的训练

  感知机

• 一个线性函数与一个激活函数的组合或者说，是在神经网络中隐藏层的一个单元（上一层的输出，下一层的输入）
• 通过最简单的激活函数进行分类判断（二分类）；0-1 激活函数，只有两种选择，将实际问题仅仅局限在了“是或不是”的角度

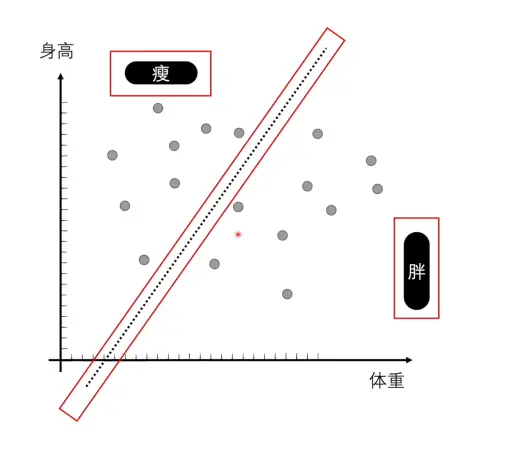
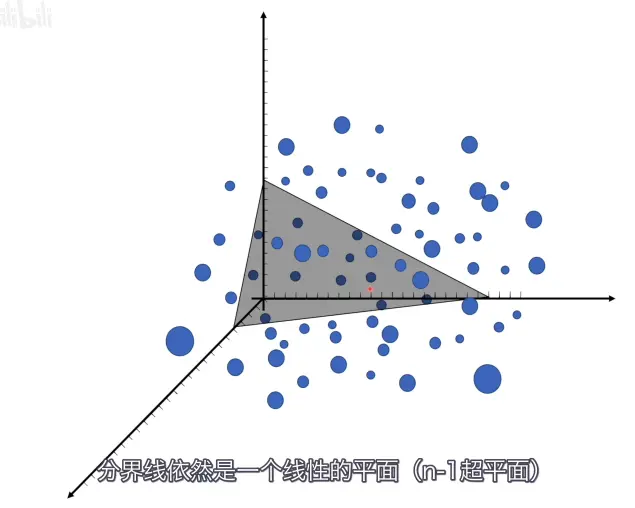
• 感知机不仅适用于二维的分类，还可以拓展至N维，都能找到如图中一样将所有的样本一分为二的分界线，如三维空间中将通过二维平面进行划分

• 公式

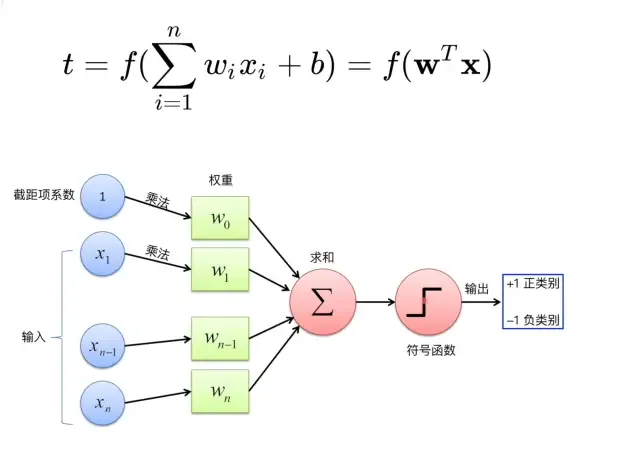
• 测试Latex语法的支持效果，以及检测BUG，hexo的LaTeX效果不如Typora，多行公式需要用 \begin{aligned} ... \end{aligned}，换行符 \\ 和定位符 &。添加了这些代码内容后，渲染正常如下

$$\begin{aligned} &\text{t即为输出，b为偏置单元，w_i为权重，x_i为输入单元}\\ & t=f(\sum_{i=1}^nw_ix_i+b)=f(\mathbf{w}^T\mathbf{x})\\ & \sum_{i=1}^nw_ix_i+b \text{正是'分界线'}\\ & \text{其数值大小无非以下，直接带入激活函数便能得到判断结果}\\ & \sum_{i=1}^nw_ix_i+b \begin{cases} \geq 0 \\[2ex] <0 \end{cases} \\ & \mathbf{w}^T\mathbf{x} ，是上一公式的简化写法，在计算机中使用向量的计算（矩阵点积） \\ \end{aligned}$$

• 尽管感知机是一个通用的’模板’，可以通过线性函数和激活函数的组合，看似能够将所有的二分问题解决，但存在一种很致命的缺陷，那就是仅靠简单的感知机将无法解决分类边界模糊或分类边界不易确定的问题，如下图这种，分界线是曲线，而不是线性的分类问题。

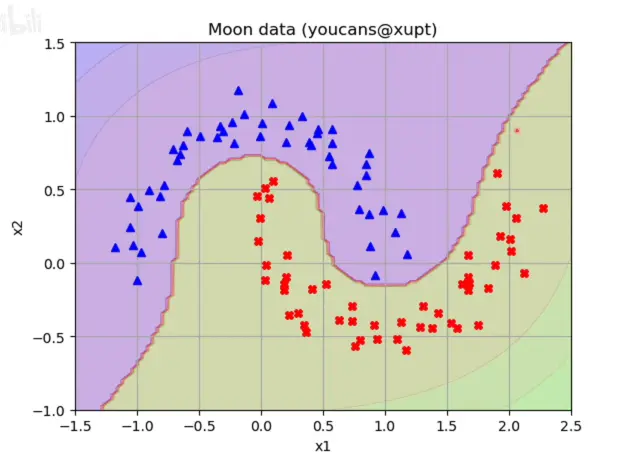
• 解决办法

  • 多个感知机的组合搭配，可为什么这样就能够解决？

    • 模板形式简单，组合也不会特别难

  • 低纬度升高纬度（待研究）

神经网络

概述与特点的理解

• 感知机的组合搭配

• 激活函数 $sigmoid$，巧妙之处在于，问题不再是判断是非，而是判断达到目标的程度有多接近（概率）

  • 通俗点说，通过激活函数，每个输出判断一个用来测试的样本有多大的概率接近期望答案（比如，给一个图片，通过神经网络来判断有多大概率是猫，如果在此基础上附加一些概率的界限，比如当是猫的概率达到90%时，那就判定得出是猫的结论）

• 输出可以变为多个目标类型，也就是可以通过训练分类出多个目标（没有绝对统一的标准，但通过不断学习接近标准）

损失函数

• 作用是定量的去衡量两个模型之间的差别，这需要计算出来

• 常见计算方法

  • 最小二乘法

    • 为何在反向传播中用梯度下降法时，最小二乘法会带来不便？

  • 极大似然估计法

    • 利用最大似然估计法的思想去寻找最接近目标期望的模型
    • 为何要前加负号反求最小值？

  • 交叉熵

    • 熵，系统的不确定性，熵值越大，不确定性越大；总系统的熵值则通过加权求和（求期望，每一部分对系统信息的贡献度不同，占比不同）

    

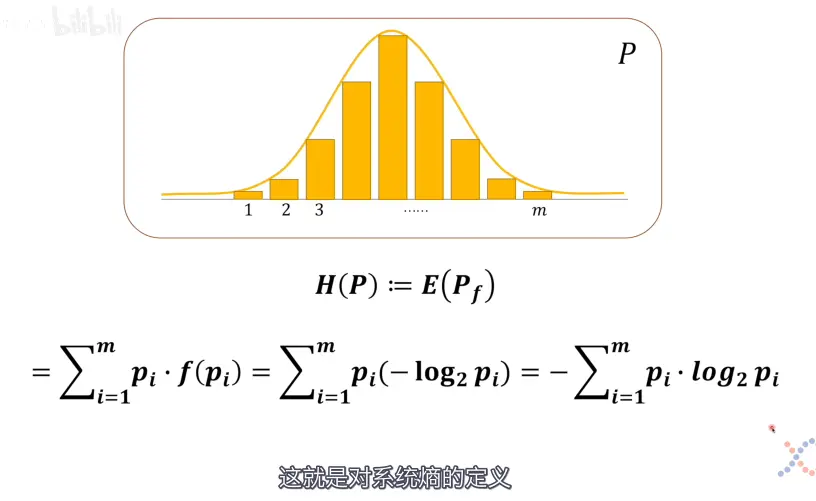
    • 散度 D~KL~ 的计算引出交叉熵的概念，下图计算的是以系统P为基准的交叉熵，由吉布斯不等式证明得出系统P的交叉熵部分的数值恒大于P的系统熵值，$H(P,Q)$ 便成了比较两个系统熵值的关键，其值越小意味着两个系统的差距越小

    

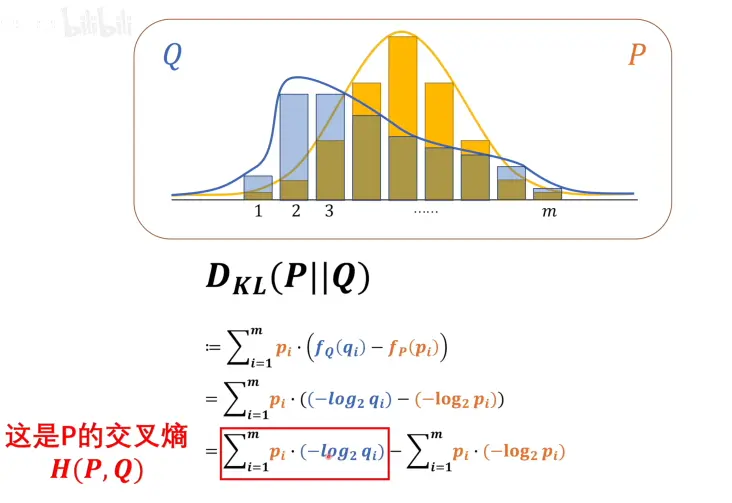
    • 交叉熵运用至神经网络的推演

    • $i$ 的数量取决于两系统的最大变量数

    • $p_i$ 表示要作为基准的模型数据，在识别猫图的例子中，就是每一张猫图的是不是猫即0和1数值标签，也是这个神经网络的输入

    • $q_i$ 表示要拿去和基准模型 比较的模型数据

    • 计算机中的信息以二进制形式存储。，$log_2(x)$ 选择 以2为底数符合了计算机中的信息量单位比特

    • 将交叉熵与极大似然估计学习联系，可以看到很多相似的地方，但存在需要谨慎对待的不同点

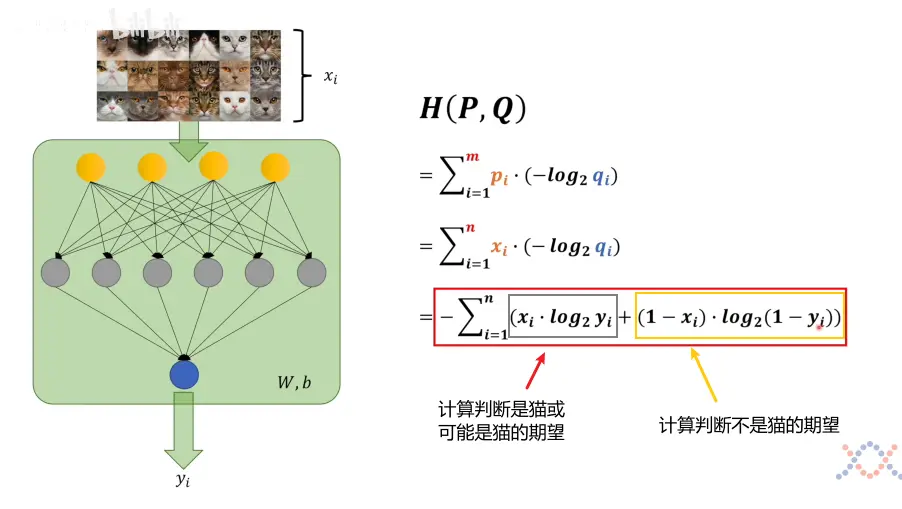
纠错，上图中红框内的公式错误，经过检索交叉熵函数的定义以及视频评论区的大佬纠错，加深了理解，可以从以下角度理解
$x_i$ 表示输入的一个标签，在判断是不是猫的项目中，其取值只有两种即$x_1$ 代表是猫，$x_2$代表不是猫，应修改公式为

• 由此我推测，对于识别多个分类的项目，是不是对应多个输入的标签来求交叉熵实现损失函数计算？

$$\begin{aligned} & H(P,Q)\\ & =-\sum_{i=1}^n (x_i·\log_2y_i)\\ & =-(x_1·\log_2y_1+x_2·\log_2y_2)\\ & x_1=1 \quad x_2=0 \quad y_2=1-y_1 \end{aligned}$$

梯度下降法

---

探究神经网络的前向传播与后向传播 的原理与公式的推导

思考一，神经网络的由来，神经网络前向传播的公式为何是这样？

• 神经网络的实现意义在于，我们能否基于给定的输入，通过某种确定的函数变换（模型）得到一个对应的输出，但有这么些特点
  • 模型不是一开始就确定的，而是通过大量的输入并与目标样本的比对来评估并且学习，最终找到合适的模型，这就是和我们人脑学习一样的过程，神经网络就是一个函数拟合器
  • 为什么要用权重×输入的方式来计算？
    • 进行结果预测的时候，权重反映了某一信息对预测的贡献度（相关性），因此当存在多个输入的时候，由于每一个输入都具有自己的权重，要具备更准确的输出，就需要加权和，对于每一项输入，计算其局部的权重×输入，最后求总和
    • 运用向量乘法实现
  • 前向传播的计算公式和过程？
    • 上一层计算得到的输出作为下一层的输入，重复这一过程直到求出最后一层的结果
    • 梯度下降，将一个维度（方向）拆分为多个分量的向量和（每一个分量都是沿着其对应的梯度方向，数值变化最快），也就是求偏导，还涉及链式求导法则
  • 后向传播的计算思路与推导？
    • 根据输出求关于输入x的梯度，链式求导，列出函数嵌套